模型评估与过拟合
学习器在训练过程中,很容易将训练样本本身的特征当作普遍特征。如在西瓜挑选问题中,如果训练样本中有很大一部分西瓜为深绿色,则学习器很大可能会将深绿色作为好瓜的评定标准之一。再比如在树叶判定过程中,如果给的叶子中有很多是有锯齿的,那么学习器很可能会将锯齿作为叶子的判定标准之一,继而产生错误的判定结果。这也称之为“过拟合”。
评估方法
很多时候我们只有D一个数据集,那么我们就需要将D进行训练集S和测试集T的划分,评估方法就是用来划分集合的方法。但是不管是什么方法都需要注意一点,训练集的数据最好不要出现在测试集中。以下是一些划分集合的方法:
留出法
将数据集D直接划分两个互斥的集合,即S|T=D,S&T=O。
注意,S和T的划分应该尽可能保持数据分布的一致性,即如果D中有1000个数据,其中700个正例和300个反例,且S有700个数据,T有300个数据,那么S最终应当有490个正例和210个反例。这种抽样方法也称之为“分层抽样”。
另外一个需要注意的问题是,单次的留出法并不可靠,每次抽样的数据有波动,那么这些不同的划分会导致不同的结果。因此一般在实际过程中需要随机多次划分,重复进行实验,最后取这些重复实验的均值最为最终结果。
留出法还有一个问题是,如果S划分的太小,那么与D的差距较大,那么测试集的结果与真实结果会有很大差别;但是如果S划分的太小,那么测试集T规模很小,最终的结果可能不稳定准确。此问题没有解决方法,一般取2/3~4/5的样本用于训练,剩余样本用于测试。
交叉验证法
将D进行分层抽样,产生多个互斥子集{D<sub>1</sub>,D<sub>2</sub>,···D<sub>k</sub>},保持每个互斥子集的分布一致性,K最常用的取值是10,此时称为10折交叉验证;其他常用的还有5、20。
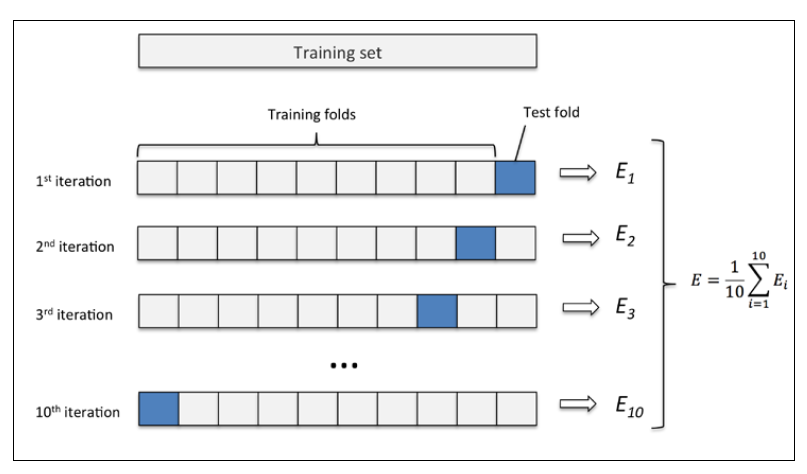
同样,交叉验证法也有和留出法一样的不稳定问题,也需要进行多次划分,常见的有10次10折交叉验证法。
若D中有m个样本数据且k=m,则称之为留1法,此方法结果比较准确,但是当m比较大的时候,计算开销太大。
自助法
假设D有m个样本,在上面的两种方法中,都需要留出一部分数据用于测试,当数据集规模比较小的时候会有很大的偏差,最后的结果会受到影响。
自助法是一个很好的解决方法。对于数据集D,每次在D中抽取一个样本复制到D',然后将其放回,重复m次后得到新样本数据集D',显然,这个新的数据集中会有一部分的重复数据,另外一部分数据则不会出现在新样本数据中。做一个简单的估计,样本在m次抽样中都不被抽取的概率是(1-1/m)<sup>m</sup>,取极限可得概论为1/e,约为36.8%。所以最终会有36.8%的数据保留作为测试数据。这个方法也成为“包外估计”。
自助法一般在数据集规模较小的时候使用,因为此方法会有估计误差。数据集规模较大的时候一般使用“留出法”和“交叉验证法”。
调参与最终模型
大多数算法都需要进行参数调节,参数配置的不同往往影响着模型性能的好坏。学习算法中的很多参数在实数范围内取值,因此对于每一个参数都建立模型是不可行的。通常的做法是:对每一个参数选定一个范围和变化步长,如选定变化范围[0,5],步长为1,那么实际要评估的参数有6个,最终从这6个候选值中产生选定值。
给定包含m个样本的数据集D,在模型评估和选择过程中由于需要留出一部分数据用于评估测试。因此,在模型选择完毕后,学习算法和参数已经选定,此时应该用数据集D重新训练模型。这个模型在训练过程中使用了所有m个样本。这才是最终我们提交给用户的模型
